Gas Laws
These are empirical laws that are used to explain the behaviour of ideal gases. An ideal gas is a perfect gas. It is a gas that does not exist, because there is no perfect situation in the real world. The Gas laws are grouped into two major categories - the physical and chemical laws. The former seek to explain the behaviour of gases based on their physical properties such as volume, temperature and pressure, while the latter do so by using their chemical properties like the number of molecules in the gases. We had looked at the chemical laws in our post - Gas Laws (Part II): Gay Lussac's & Avogadro's Laws, so this post will be devoted to the discussion on the physical laws.
Boyle's Law
This law states that the volume, V, of a given mass of gas is inversely proportional to its pressure, P, provided the temperature remains constant. This implies that if the volume of a gas is doubled, it will lead to a decrease in the gas pressure by half. Similarly, if the volume of the gas is decreased by half, the pressure exerted by its molecules on the walls of the containing vessel will increase. This is because the area of the containing vessel available for collision has been reduced, thereby increasing the force per unit area.
Mathematically, Boyle's Law can be expressed as:
V & 1/P (at constant T)
V = k/P ....................(i)
k = PV .....................(ii)
V = k/P ....................(i)
k = PV .....................(ii)
From equation (i), a plot of V against 1/P will give a straight line graph which passes through the origin. Click here to see all the graph variants of Boyle's Law.
According to equation (ii), the product of the volume and pressure of a gas at constant temperature will always give a constant. Hence, for a given mass of gas whose volume is V1 at pressure, P1, and V2 at pressure, P2, we can conclude that:
P1V1 = P2V2 ............................(iii)
Note that the volume can be in m^3, cm^3 or dm^3, while the pressure can be in mm Hg (millimetres mercury), atm (atmospheres) or Nm^-2 (Newton per metre). The most important thing is the consistency of units. The following conversion factors can be of help:
1 dm^3 = 1000 cm^3 = 10^-3 m^3
1 atm = 760 mm Hg = 101325 Nm^-2
1 atm = 760 mm Hg = 101325 Nm^-2
Example 1
50 cm^3 of oxygen at 20 atmospheres pressure is placed in a 30 cm^3 container. Calculate the new pressure if temperature is kept constant.
50 cm^3 of oxygen at 20 atmospheres pressure is placed in a 30 cm^3 container. Calculate the new pressure if temperature is kept constant.
Answer
This question involves changes in volume and pressure only at constant temperature; therefore, we will apply the Boyle's law:
This question involves changes in volume and pressure only at constant temperature; therefore, we will apply the Boyle's law:
P1V1 = P2V2,
where
P1 - initial pressure = 20 atm,
V1 - initial volume = 50 cm^3,
V2 - final volume = 30 cm^3,
P2 - final pressure = ?
V1 - initial volume = 50 cm^3,
V2 - final volume = 30 cm^3,
P2 - final pressure = ?
Making P2 subject of the formula gives:
P2 = P1V1/V2
= 20 × 50/30
= 33.33 atm
= 20 × 50/30
= 33.33 atm
Example 2
A given mass of a gas occupies a volume of 250 cm^3 at a pressure of 740 mm Hg. What will be its volume at atmospheric pressure?
A given mass of a gas occupies a volume of 250 cm^3 at a pressure of 740 mm Hg. What will be its volume at atmospheric pressure?
Answer
The question also involves changes in pressure and volume only. So, using Boyle's law:
The question also involves changes in pressure and volume only. So, using Boyle's law:
P1V1 = P2V2,
where,
P1 - initial pressure = 740 mm Hg,
V1 - initial volume = 250 cm^3,
P2 - final pressure = 760 mm Hg, (atmospheric pressure)
V2 - final volume = ?
V1 - initial volume = 250 cm^3,
P2 - final pressure = 760 mm Hg, (atmospheric pressure)
V2 - final volume = ?
V2 = P1V1/P2
= 740 × 250/760
= 243. 42 cm^3
= 740 × 250/760
= 243. 42 cm^3
Charles' Law
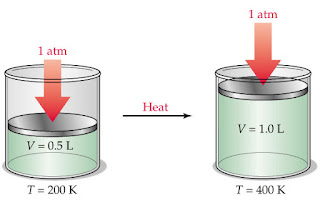
This law states that the volume, V, of a fixed mass of gas is directly proportional to its absolute temperature, T, provided the pressure remains constant. This implies that an increase in the temperature of a gas will lead to a corresponding increase in the volume of the gas, and vice versa.
According to the kinetic theory of gases, the temperature of a gas is a measure of the average kinetic energy of the gas molecules. That is to say, an increase in the temperature of a gas will increase the kinetic energies of its molecules, thereby making them to collide more often, and increasing their force of collision, F, with the walls of the containing vessel. In order for the pressure to remain constant, there must be an expansion in the surface area of the containing vessel, so that F/A = constant. This expansion is in the form of an increase in height of the surface area, which translates to an increase in volume. ( Given that volume = area × height).
Mathematically, Charles' Law can be expressed as:
V & T (at constant P)
V = kT .............................(iv)
k = V/T .............................(v)
V = kT .............................(iv)
k = V/T .............................(v)
From equation (v), the volume - temperature ratio of a gas at constant pressure gives a constant. Therefore, for a given mass of gas whose volume is V1 at temperature, T1, and V2 at temperature, T2, then:
V1/T1 = V2/T2 ............................(vi)
Absolute Temperature & Absolute Zero
Absolute temperature is the temperature value based on the Kelvin scale. Hence, every temperature involved in the Gas Laws calculations MUST always be converted to the Kelvin temperature by adding 273 to the Celsius temperature because 0°C = 273K.
Absolute temperature is the temperature value based on the Kelvin scale. Hence, every temperature involved in the Gas Laws calculations MUST always be converted to the Kelvin temperature by adding 273 to the Celsius temperature because 0°C = 273K.
K = °C + 273; similarly, °C = K - 273
On the other hand, absolute zero, i.e,0K or -273°C, is the temperature at which the volume of a gas is considered to be 0 cm^3. According to Charles' Law, at that temperature, the gas is expected to varnish, since its volume is directly proportional to the temperature as depicted in the graph of V against T(°C).
However, studies have shown that no existing gas varnishes at extremely low temperatures, rather all known gases liquefy at temperatures below 273K, because they are not ideal gases. Therefore, Charles' & Boyle's Laws are only true for ideal gases, but fail for real gases.
Example 3
If the volume of a given mass of gas at 0°C is 30.7 cm^3, what will be the volume of the gas at 20°C, pressure remaining constant?
If the volume of a given mass of gas at 0°C is 30.7 cm^3, what will be the volume of the gas at 20°C, pressure remaining constant?
Answer
This is a question that involves changes in volume and temperature at constant pressure. Hence, Charles' Law is applicable:
V1/T1 = V2/T2
where,
V1 - initial volume = 30.7 cm^3,
T1 - initial temperature =0°C + 273
= 273K,
T2 - final temperature = 20°C + 273
= 293K,
V2 - final volume = ?
T1 - initial temperature =0°C + 273
= 273K,
T2 - final temperature = 20°C + 273
= 293K,
V2 - final volume = ?
V2 = V1T2/T1
= 30.7 × 293/273
= 32.95 cm^3
= 30.7 × 293/273
= 32.95 cm^3
Example 4
A given quantity of gas occupies 5.0 dm^3 at 250K. At what temperature will its volume be doubled keeping the pressure constant?
A given quantity of gas occupies 5.0 dm^3 at 250K. At what temperature will its volume be doubled keeping the pressure constant?
Answer
Applying Charles' Law:
Applying Charles' Law:
V1/T1 = V2/T2, where
V1 - initial volume = 5.0 dm^3,
T1 - initial temperature = 250K,
V2 - final volume = 2 × V1
= 2 × 5
= 10.0 dm^3
T2 - final temperature = ?
T1 - initial temperature = 250K,
V2 - final volume = 2 × V1
= 2 × 5
= 10.0 dm^3
T2 - final temperature = ?
T2 = V2T1/V1
= 10 × 250/5
= 500K
= 10 × 250/5
= 500K
General Gas Equation
The general gas equation is a combination of Boyle's and Charles' Laws as shown below:
V & T (Charles)
V & 1/P (Boyle)
V & 1/P (Boyle)
Combining both using joint variation,
V & T/P
V = KT/P ....................................(vii)
PV/T = k .....................................(viii)
V = KT/P ....................................(vii)
PV/T = k .....................................(viii)
Analysing a given mass of gas, under two different sets of conditions based on equation (viii), we will obtain:
P1V1/T1 = P2V2/T2 ....................(ix)
Standard Temperature & Pressure (s.t.p.)
Since the volume of a gas varies with temperature, and the room temperature varies from one location or country to another due to climatic variations; there was a need by scientists all over the world, to establish standard conditions under which experimental studies involving gases can be carried out in order to obtain consistent results, irrespective of the location. These conditions were a temperature of 273K and a pressure of 1 atm/760 mm Hg/101325 Nm^-2 and are considered to be the standard temperature & pressure (s.t.p.).
Since the volume of a gas varies with temperature, and the room temperature varies from one location or country to another due to climatic variations; there was a need by scientists all over the world, to establish standard conditions under which experimental studies involving gases can be carried out in order to obtain consistent results, irrespective of the location. These conditions were a temperature of 273K and a pressure of 1 atm/760 mm Hg/101325 Nm^-2 and are considered to be the standard temperature & pressure (s.t.p.).
Example 5
12.0 dm^3 of a gas at s.t.p was subjected by means of a movable piston to two times the original pressure with the temperature being now kept at 384K. What is the volume of the gas in dm^3 at this pressure?
12.0 dm^3 of a gas at s.t.p was subjected by means of a movable piston to two times the original pressure with the temperature being now kept at 384K. What is the volume of the gas in dm^3 at this pressure?
Answer
Since the question involves changes in volume, temperature and pressure, then, we will make use of the general gas equation:
Since the question involves changes in volume, temperature and pressure, then, we will make use of the general gas equation:
P1V1/T1 = P2V2/T2
where,
P1 - initial pressure = 760 mm Hg (standard pressure),
V1 - initial volume = 12.0 dm^3,
T1 - initial temperature = 273K (standard temperature),
P2 - final pressure = 2 × P1
= 2 × 760 = 1520 mm Hg,
T2 - final temperature = 384K,
V2 - final volume = ?
V1 - initial volume = 12.0 dm^3,
T1 - initial temperature = 273K (standard temperature),
P2 - final pressure = 2 × P1
= 2 × 760 = 1520 mm Hg,
T2 - final temperature = 384K,
V2 - final volume = ?
V2 = P1V1T2/P2T1
= (760 × 12 × 384)/(1520 × 273)
= 8.44 dm^3
= (760 × 12 × 384)/(1520 × 273)
= 8.44 dm^3
Example 6
If a gas occupies a container of volume 165 cm^3 at 27°C and 0.984 atm, calculate its volume in cm^3 at s.t.p.
If a gas occupies a container of volume 165 cm^3 at 27°C and 0.984 atm, calculate its volume in cm^3 at s.t.p.
Answer
Applying the general gas equation:
Applying the general gas equation:
P1V1/T1 = P2V2/T2
where,
P1 - initial pressure = 0.984 atm,
V1 - initial volume = 165 cm^3,
T1 - initial temperature = 27°C + 273
= 300K,
P2 - final pressure = 1 atm,
T2 - final temperature = 273K,
V2 - final volume = ?
V1 - initial volume = 165 cm^3,
T1 - initial temperature = 27°C + 273
= 300K,
P2 - final pressure = 1 atm,
T2 - final temperature = 273K,
V2 - final volume = ?
V2 = P1V1T2/P2T1
= (0.984 × 165 × 273)/(1 × 300)
= 147.75 cm^3
= (0.984 × 165 × 273)/(1 × 300)
= 147.75 cm^3
Example 7
At 25°C and 1 atm, a gas occupies a volume of 1.50 dm^3. What volume will it occupy at 100°C and 5 atm?
At 25°C and 1 atm, a gas occupies a volume of 1.50 dm^3. What volume will it occupy at 100°C and 5 atm?
Answer
Using the general gas equation:
Using the general gas equation:
P1V1/T1 = P2V2/T2
where,
P1 - initial pressure = 1 atm,
V1 - initial volume = 1.5 dm^3,
T1 - initial temperature = 25°C + 273
= 298K,
P2 - final pressure = 5 atm,
T2 - final temperature = 100°C + 273
= 373K,
V2 - final volume = ?
V1 - initial volume = 1.5 dm^3,
T1 - initial temperature = 25°C + 273
= 298K,
P2 - final pressure = 5 atm,
T2 - final temperature = 100°C + 273
= 373K,
V2 - final volume = ?
V2 = P1V1T2/P2T1
= (1 × 1.5 × 373)/(5 × 298)
= 0.376 dm^3
= (1 × 1.5 × 373)/(5 × 298)
= 0.376 dm^3
Ideal Gas Equation
Since the ratio PV/T equals to a constant, according to the general gas equation (equation (viii)), then the ideal gas equation can be given as:
PV = nRT ...................................(x)
where,
P = pressure in atm
V = volume in dm^3
T = temperature in K
n = number of moles
R = molar gas constant (0.082 atm dm^3 mol^-1 K^-1)
V = volume in dm^3
T = temperature in K
n = number of moles
R = molar gas constant (0.082 atm dm^3 mol^-1 K^-1)
For 1 mole of a gas at s.t.p,
standard pressure = 1atm
standard temperature = 273K
volume occupied by 1 mole of a gas = 22.4 dm^3
standard pressure = 1atm
standard temperature = 273K
volume occupied by 1 mole of a gas = 22.4 dm^3
Therefore,
R = PV/nT
= (1 × 22.4)/(1 × 273)
= 22.4/273
= 0.082 atm dm^3 mol^-1 K^-1
= (1 × 22.4)/(1 × 273)
= 22.4/273
= 0.082 atm dm^3 mol^-1 K^-1
Alternatively, if standard pressure = 101325 Nm^-2, and volume = 0.0224 m^3
then,
R = (101325 × 22.4)/(1 × 273)
= 2269.98/273
= 8.314 J mol^-1 K^-1
= 2269.98/273
= 8.314 J mol^-1 K^-1
If we divide both sides of equation (x) with V, we will obtain:
PV/V = nRT/V
P = (n/V) RT ........................(xi)
P = (n/V) RT ........................(xi)
Recall, concentration in mol dm^-3, C = n/V ......(xii)
Substituting equation (xii) into (xi) gives us:
P = CRT ......................................(xiii)
Equation (x) gives the ideal gas equation in terms of pressure, volume, temperature and no. of moles, while equation (xiii) gives the equation in terms of pressure, concentration and temperature.
The ideal gas equation holds true for all gases because, according to the Avogadro's Law, equal volume of gases contain equal number of molecules at the same temperature and pressure.
Example 8
5.0 moles of an ideal gas are at temperature of –33°C and a pressure of 350 torrs. What volume in dm^3 will the gas occupy at that temperature? (R = 0.082 atm dm^3 mol^-1 K^-1, 1 torr = 1 atm)
5.0 moles of an ideal gas are at temperature of –33°C and a pressure of 350 torrs. What volume in dm^3 will the gas occupy at that temperature? (R = 0.082 atm dm^3 mol^-1 K^-1, 1 torr = 1 atm)
Answer
Since the question involves moles, pressure, temperature and volume, then, the right equation to apply is the ideal gas equation.
Since the question involves moles, pressure, temperature and volume, then, the right equation to apply is the ideal gas equation.
PV = nRT
where,
P - pressure = 350 atm
T - temperature = –33°C + 273 = 240K
n - number of moles = 5.0 moles
R - molar gas constant = 0.082 atm dm^3 mol^-1 K^-1
V - volume = ?
T - temperature = –33°C + 273 = 240K
n - number of moles = 5.0 moles
R - molar gas constant = 0.082 atm dm^3 mol^-1 K^-1
V - volume = ?
V = nRT/P
= 5 × 0.082 × 240/350
= 0.28 dm^3
= 5 × 0.082 × 240/350
= 0.28 dm^3
Example 9
Calculate the number of moles of gas, which occupies 500 dm^3 at temperature of 77°C and pressure of 2.52 × 10^5 Nm^-2.(R = 8.314 J mol^-1 K^-1)
Calculate the number of moles of gas, which occupies 500 dm^3 at temperature of 77°C and pressure of 2.52 × 10^5 Nm^-2.(R = 8.314 J mol^-1 K^-1)
Answer
Using the ideal gas equation:
Using the ideal gas equation:
PV = nRT
where,
P - pressure = 2.52 × 10^5 Nm^-2
T - temperature = 77°C + 273 = 350K
R - molar gas constant = 8.314 J mol^-1 K^-1
V - volume = 500 dm^3 = 500 × 10^-3 m^3 (since pressure is in Nm^-2, volume must be in m^3)
n - number of moles = ?
T - temperature = 77°C + 273 = 350K
R - molar gas constant = 8.314 J mol^-1 K^-1
V - volume = 500 dm^3 = 500 × 10^-3 m^3 (since pressure is in Nm^-2, volume must be in m^3)
n - number of moles = ?
n = PV/RT
= 2.52 × 10^5 × 500 × 10^-3/8.314 × 350
= 252000 × 0.5/8.314 × 350
= 43.30 moles
= 2.52 × 10^5 × 500 × 10^-3/8.314 × 350
= 252000 × 0.5/8.314 × 350
= 43.30 moles
Dalton's Law of Partial Pressure
This law states that in a mixture of gases that are not chemically combined, the total pressure of the gas mixture is the sum of the partial pressure of the individual gases that make up the mixture. If Ptotal is the total pressure of a mixture of gases A, B, C...n, and Pa, Pb, Pc....Pn are the partial pressures due to gases A, B, C....n, then,
Ptotal = Pa + Pb + Pc + .... + Pn ........(xiv)
but,
Pa = na/ntotal × Ptotal
Pb = nb/ntotal × Ptotal
Pc = nc/ntotal × Ptotal
Pb = nb/ntotal × Ptotal
Pc = nc/ntotal × Ptotal
where,
na, nb, and nc = number of moles (molecules) of gases A, B and C in the mixture; and na/ntotal, nb/ntotal, nc/ntotal are the mole fractions of gases A, B and C respectively.
ntotal = total number of moles (molecules) of gases in the mixture (na + nb + nc....)
For instance, the total pressure exerted by air (made up of nitrogen, oxygen, carbon (IV) oxide, noble gases, water vapour and others) in a container, is the sum of partial pressure exerted by each of the gases listed above, assuming each of them was to act alone in the containing vessel.
Usually, most gases prepared in the laboratory are collected over water. If the pressure of the collected gas is measured at a given temperature, it would be observed that it contains the saturated vapour pressure (s.v.p) of water at that temperature, and as such, the measured pressure is not the true pressure of the dry gas. Therefore, to get the actual pressure of the dry gas (partial pressure), the s.v.p of water must be subtracted from the pressure of the wet gas (total pressure); i.e,
Pressure of Dry Gas = Pressure of Wet Gas - Saturated Vapour Pressure of H2O .............(xv)
Example 10
What is the partial pressure of hydrogen gas collected over water at standard atmospheric pressure and 35°C if the saturated vapour pressure of water is 30 mm Hg at that temperature?
What is the partial pressure of hydrogen gas collected over water at standard atmospheric pressure and 35°C if the saturated vapour pressure of water is 30 mm Hg at that temperature?
Answer
Partial Pressure of H2 gas = Total (Atmospheric) Pressure, Ptotal - S.V.P of H20 at 35°C
Partial Pressure of H2 gas = Total (Atmospheric) Pressure, Ptotal - S.V.P of H20 at 35°C
partial pressure of H2 = 760 - 30
= 730 mm Hg
= 730 mm Hg
Example 11
A gaseous mixture of 40.0g of oxygen and 28.0g of nitrogen has a total pressure of 1.8 atm. Calculate the partial pressure of oxygen in the mixture (O = 16, N = 14)
A gaseous mixture of 40.0g of oxygen and 28.0g of nitrogen has a total pressure of 1.8 atm. Calculate the partial pressure of oxygen in the mixture (O = 16, N = 14)
Answer
Mass of O2 in gaseous mixture = 40g
Moles of O2 = Mass of O2/Molecular mass of O2
= 40/(16 × 2) = 40/32
= 1.25 moles
Mass of O2 in gaseous mixture = 40g
Moles of O2 = Mass of O2/Molecular mass of O2
= 40/(16 × 2) = 40/32
= 1.25 moles
Similarly,
Mass of N2 in gaseous mixture = 28g
Moles of N2 = Mass of N2/Molecular mass of N2
= 28/(14 × 2) = 28/28
= 1.00 moles
Moles of N2 = Mass of N2/Molecular mass of N2
= 28/(14 × 2) = 28/28
= 1.00 moles
Total number of moles of gaseous mixture = no. of moles of O2 + no. of moles of N2
= 1.25 + 1.00 = 2.25 moles
= 1.25 + 1.00 = 2.25 moles
Total pressure of mixture = 1.8 atm
Therefore,
Partial pressure of O2 in mixture = mole fraction of O2 × total pressure
= (1.25/2.25) × 1.8
= 1.0 atm
Example 12
50 cm^3 of hydrogen was collected over water at 25°C and 790 mm Hg. If the vapour pressure of water at the temperature of the experiment was 15 mm Hg, calculate the volume of the gas at 750 mm Hg and 15°C.
50 cm^3 of hydrogen was collected over water at 25°C and 790 mm Hg. If the vapour pressure of water at the temperature of the experiment was 15 mm Hg, calculate the volume of the gas at 750 mm Hg and 15°C.
Answer
This question is a combination of the general gas equation and Dalton's Law of Partial Pressure. The first thing to do is to determine the partial pressure of the hydrogen gas collected over water, and then use the result as the initial pressure in the general gas equation.
This question is a combination of the general gas equation and Dalton's Law of Partial Pressure. The first thing to do is to determine the partial pressure of the hydrogen gas collected over water, and then use the result as the initial pressure in the general gas equation.
Given:
Total pressure = 790 mm Hg
Vapour pressure of water = 15 mm Hg
Initial volume, V1 = 50 cm^3
Initial temperature, T1 = 25°C + 273 = 298K
Final pressure, P2 = 750 mm Hg
Final temperature, T2 = 15°C + 273 = 288K
Final volume, V2 = ?
Total pressure = 790 mm Hg
Vapour pressure of water = 15 mm Hg
Initial volume, V1 = 50 cm^3
Initial temperature, T1 = 25°C + 273 = 298K
Final pressure, P2 = 750 mm Hg
Final temperature, T2 = 15°C + 273 = 288K
Final volume, V2 = ?
but,
Initial pressure, P1 = partial pressure of hydrogen
= total pressure - vapour pressure of water
= 790 - 15 = 775 mm Hg
= total pressure - vapour pressure of water
= 790 - 15 = 775 mm Hg
Applying the general gas equation and substituting the values of the parameters into the equation gives:
P1V1/T1 = P2V2/T2
V2 = P1V1T2/P2T1
= (775 × 50 × 288)/(750 × 298)
= 49.93 cm^3
V2 = P1V1T2/P2T1
= (775 × 50 × 288)/(750 × 298)
= 49.93 cm^3
Do These
Question 1
To what temperature must a gas at 273K be heated in order to double both its volume and pressure?
To what temperature must a gas at 273K be heated in order to double both its volume and pressure?
Question 2
The ratio of the initial to the final pressure of a given mass of gas is 1:1.5. Calculate the final volume of the gas if the initial volume was 450 cm^3 at the same temperature.
The ratio of the initial to the final pressure of a given mass of gas is 1:1.5. Calculate the final volume of the gas if the initial volume was 450 cm^3 at the same temperature.
Question 3
The pressure of 100 cm^3 of oxygen at 35°C is 750 mm Hg. What will be the volume of the gas if the pressure is reduced to 100 mm Hg at 25°C?
The pressure of 100 cm^3 of oxygen at 35°C is 750 mm Hg. What will be the volume of the gas if the pressure is reduced to 100 mm Hg at 25°C?
Question 4
A mixture of 0.40 mole of argon, 0.30 mole of helium and 0.50 mole of nitrogen exerts a total pressure of 3.5 atm. What is the partial pressure of nitrogen in the mixture?
A mixture of 0.40 mole of argon, 0.30 mole of helium and 0.50 mole of nitrogen exerts a total pressure of 3.5 atm. What is the partial pressure of nitrogen in the mixture?
Question 5
The partial pressure of oxygen in a sample of air is 350 mm Hg and the total pressure is 785 mm Hg. What is the mole fraction of oxygen?
The partial pressure of oxygen in a sample of air is 350 mm Hg and the total pressure is 785 mm Hg. What is the mole fraction of oxygen?
Question 6
50cm^3 of a gas at 45°C is warmed to 85°C at a fixed pressure, what is the fractional increase in volume of the gas?
50cm^3 of a gas at 45°C is warmed to 85°C at a fixed pressure, what is the fractional increase in volume of the gas?
Question 7
75 cm^3 of a gas was collected over water at 20°C and 785 mm Hg. Calculate the volume of the gas at s.t.p, if the saturated vapour pressure of water at 20°C is 25 mm Hg.
75 cm^3 of a gas was collected over water at 20°C and 785 mm Hg. Calculate the volume of the gas at s.t.p, if the saturated vapour pressure of water at 20°C is 25 mm Hg.
Question 8
300 cm^3 of a gas at 25°C exerts a pressure of 750 mm Hg. Calculate its pressure if its volume increases to 450 cm^3 at 75°C.
300 cm^3 of a gas at 25°C exerts a pressure of 750 mm Hg. Calculate its pressure if its volume increases to 450 cm^3 at 75°C.
Question 9
Find the volume occupied by 16.0g of oxygen under a pressure of 3.5 × 10^5 Nm^-2 at a temperature of 27°C. (Molar gas constant = 8.314 J mol^-1 K^-1, O = 16)
Find the volume occupied by 16.0g of oxygen under a pressure of 3.5 × 10^5 Nm^-2 at a temperature of 27°C. (Molar gas constant = 8.314 J mol^-1 K^-1, O = 16)
Twitter: @gmtacademy
WhatsApp: 07034776117
Facebook: www.facebook.com/greatermindstutors
WhatsApp: 07034776117
Facebook: www.facebook.com/greatermindstutors

Wnopueter-me-1978 Troy Lofgreen https://wakelet.com/wake/cpqstZ65ddlWRBKYY_AM5
ReplyDeletesnoopvicensio
AnaepieXstite-1983 Charlie Horne FixMeStick
ReplyDeleteAVG PC TuneUp
Nulled
ilamriada
The blogpost provides a comprehensive introduction to gas laws, focusing on Boyle's Law and Charles' Law. The explanations are clear and concise, making it easy to understand the fundamental principles behind gas behavior. It's a great starting point for anyone looking to delve into the world of gas laws. Many other students misunderstood the topic with improper guidance. If you want a deep knowledge of the topic then you must learn from well-skilled and efficient physics tuition.
ReplyDelete